Continuation of metallic solutions using preblur
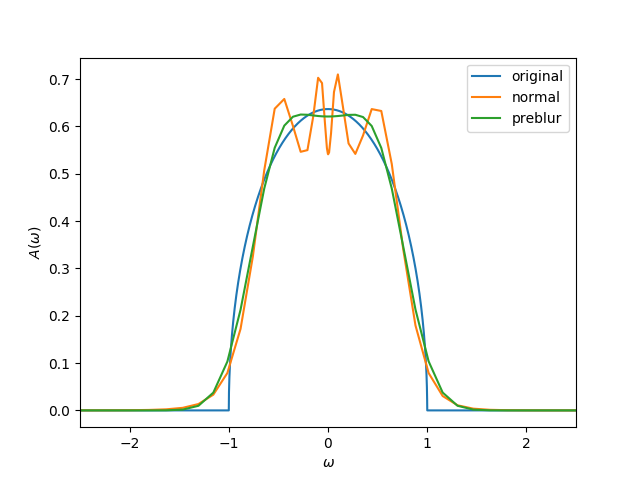
The MaxEnt formalism has the tendency of producing spurious noise around the \(\omega=0\) point. This is usually not problematic for insulating solutions, but not desirable for metallic spectral functions.
One strategy to tackle this is the so-called preblur technique [1]. There, a so-called hidden image \(H\) is introduced, with the spectral function being \(A = B H\) [2]. The matrix \(B\) is the blur matrix; multiplying by \(B\) is equal to a convolution with a Gaussian (its width \(b\) is an external parameter). Then, in the cost function, both \(H\) and \(A\) are used,
The parametrization \(H(v)\) is, e.g., Bryan’s parametrization, \(H(v) = D e^{Vv}\). The parametrization \(A(H)\) is, of course, \(A = B H\).
The class MaxEntCostFunction accepts a parameter A_of_H.
Only two different parametrizations for \(A(H)\) are implemented: the IdentityA_of_H and PreblurA_of_H variants.
The former just chooses the usual \(A(H) = H\), the latter uses \(A(H) = BH\) as discussed here.
Note that, for performance reasons, the kernel has to be redefined to include the blur matrix. This is done by choosing the PreblurKernel.
The calculation should be performed using different values for \(b\). The best value of \(b\) can be determined similarly to determining \(\alpha\); e.g., by calculating the probability of every \(b\) or by looking at \(\log(\chi^2)\) of \(\log b\).
Example
A full example:
1
2from triqs_maxent.analyzers.linefit_analyzer import fit_piecewise
3
4try:
5 # TRIQS 2.1
6 from triqs.gf import *
7 GfImFreq
8except NameError:
9 # TRIQS 1.4
10 from triqs.gf.local import *
11from triqs_maxent import *
12from triqs_maxent.analyzers.linefit_analyzer import fit_piecewise
13
14# whether we want to save and plot the results
15save = False
16plot = True
17
18# construct a test Green function
19# for reference, G(w)
20G_w = GfReFreq(window=(-3, 3), indices=[0])
21G_w << SemiCircular(1)
22
23# the G(iw)
24G_iw = GfImFreq(beta=40, indices=[0], n_points=50)
25G_iw << SemiCircular(1)
26
27# we inverse Fourier-transform G(iw) to G(tau)
28G_tau = GfImTime(beta=G_iw.beta, indices=[0], n_points=102)
29G_tau.set_from_fourier(G_iw)
30# and add some noise (MaxEnt does not work without noise)
31G_tau.data[:, 0, 0] = G_tau.data[:, 0, 0] + \
32 1.e-4 * np.random.randn(len(G_tau.data))
33
34tm = TauMaxEnt()
35# the following allows to Ctrl-C the calculation and choose what to do
36tm.interactive = True
37tm.set_G_tau(G_tau)
38# set an appropriate alpha mesh
39tm.alpha_mesh = LogAlphaMesh(alpha_min=0.08, alpha_max=1000, n_points=30)
40tm.set_error(1.e-4)
41
42# run without preblur
43result_normal = tm.run()
44last_result = result_normal
45
46K_tau = tm.K
47
48# loop over different values of the preblur parameter b
49results_preblur = {}
50for b in [0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4]:
51 print('Running for b = {}'.format(b))
52 tm.A_of_H = PreblurA_of_H(b=b, omega=tm.omega)
53 tm.K = PreblurKernel(K=K_tau, b=b)
54 # initialize A(w) with the last result, this leads to faster convergence
55 tm.A_init = last_result.analyzer_results['LineFitAnalyzer']['A_out']
56 results_preblur[b] = tm.run()
57 last_result = results_preblur[b]
58
59# save the results
60if save:
61 from h5 import HDFArchive
62 with HDFArchive('preblur.h5', 'w') as ar:
63 ar['result_normal'] = result_normal.data
64 ar['results_preblur'] = [r.data for r in results_preblur]
65
66# extract the chi2 value from the optimal alpha for each blur parameter
67chi2s = []
68# we have to reverse-sort it because fit_piecewise expects it in that order
69b_vals = sorted(list(results_preblur.keys()), reverse=True)
70for b in b_vals:
71 r = results_preblur[b]
72 alpha_index = r.analyzer_results['LineFitAnalyzer']['alpha_index']
73 chi2s.append(r.chi2[alpha_index])
74
75# perform a linefit to get the optimal b value
76b_index, _ = fit_piecewise(np.log10(b_vals), np.log10(chi2s))
77b_ideal = b_vals[b_index]
78print('Ideal b value = ', b_ideal)
79
80if plot:
81 import matplotlib.pyplot as plt
82 from triqs.plot.mpl_interface import oplot
83 oplot(G_w, mode='S')
84 result_normal.analyzer_results['LineFitAnalyzer'].plot_A_out()
85 results_preblur[b_ideal].analyzer_results['LineFitAnalyzer'].plot_A_out()
86 plt.xlabel(r'$\omega$')
87 plt.ylabel(r'$A(\omega)$')
88 plt.legend(['original', 'normal', 'preblur'])
89 plt.xlim(-2.5, 2.5)
90 plt.savefig('preblur_A.png')
91 plt.show()
Footnotes