SrVO3 (single-shot)

We will discuss now how to set up a full working calculation, including the initialization of the CTHYB solver. Some additional parameter are introduced to make the calculation more efficient. This is a more advanced example, which is also suited for parallel execution. The conversion, which we assume to be carried out already, is discussed here.

For the convenience of the user, we provide also two working python scripts in this documentation. One for a calculation using Kanamori definitions (dft_dmft_cthyb.py) and one with a rotational-invariant Slater interaction Hamiltonian (dft_dmft_cthyb_slater.py). The user has to adapt these scripts to his own needs.

Loading modules

First, we load the necessary modules:

from pytriqs.applications.dft.sumk_dft import *
from pytriqs.gf.local import *
from pytriqs.archive import HDFArchive
from pytriqs.operators.util import *
from pytriqs.applications.impurity_solvers.cthyb import *

The last two lines load the modules for the construction of the CTHYB solver.

Initializing SumkDFT

We define some parameters, which should be self-explanatory:

dft_filename = 'SrVO3'          # filename
U = 4.0                         # interaction parameters
J = 0.65
beta = 40                       # inverse temperature
loops = 15                      # number of DMFT loops
mix = 0.8                       # mixing factor of Sigma after solution of the AIM
dc_type = 1                     # DC type: 0 FLL, 1 Held, 2 AMF
use_blocks = True               # use bloc structure from DFT input
prec_mu = 0.0001                # precision of chemical potential

And next, we can initialize the SumkDFT class:

SK = SumkDFT(hdf_file=dft_filename+'.h5',use_dft_blocks=use_blocks)

Initializing the solver

We also have to specify the CTHYB solver related settings. We assume that the DMFT script for SrVO3 is executed on 16 cores. A sufficient set of parameters for a first guess is:

p = {}
# solver
p["random_seed"] = 123 * mpi.rank + 567
p["length_cycle"] = 200
p["n_warmup_cycles"] = 100000
p["n_cycles"] = 1000000
# tail fit
p["perform_tail_fit"] = True
p["fit_max_moment"] = 4
p["fit_min_n"] = 30
p["fit_max_n"] = 60

Here we use a tail fit to deal with numerical noise of higher Matsubara frequencies. For other options and more details on the solver parameters, we refer the user to the CTHYB solver documentation. It is important to note that the solver parameters have to be adjusted for each material individually. A guide on how to set the tail fit parameters is given below.

The next step is to initialize the solver class. It consist of two parts:

1. Calculating the multi-band interaction matrix, and constructing the interaction Hamiltonian.
2. Initializing the solver class itself.

The first step is done using methods of the TRIQS library:

n_orb = SK.corr_shells[0]['dim']
l = SK.corr_shells[0]['l']
spin_names = ["up","down"]
orb_names = [i for i in range(n_orb)]
# Use GF structure determined by DFT blocks:
gf_struct = SK.gf_struct_solver[0]
# Construct U matrix for density-density calculations:
Umat, Upmat = U_matrix_kanamori(n_orb=n_orb, U_int=U, J_hund=J)

We assumed here that we want to use an interaction matrix with Kanamori definitions of \(U\) and \(J\).

Next, we construct the Hamiltonian and the solver:

h_int = h_int_density(spin_names, orb_names, map_operator_structure=SK.sumk_to_solver[0], U=Umat, Uprime=Upmat)
S = Solver(beta=beta, gf_struct=gf_struct)

As you see, we take only density-density interactions into account. Other Hamiltonians with, e.g. with full rotational invariant interactions are:

• h_int_kanamori
• h_int_slater

For other choices of the interaction matrices (e.g Slater representation) or Hamiltonians, we refer to the reference manual of the TRIQS library.

DMFT cycle

Now we can go to the definition of the self-consistency step. It consists again of the basic steps discussed in the previous section, with some additional refinements:

for iteration_number in range(1,loops+1):
    if mpi.is_master_node(): print "Iteration = ", iteration_number

    SK.symm_deg_gf(S.Sigma_iw,orb=0)                        # symmetrizing Sigma
    SK.set_Sigma([ S.Sigma_iw ])                            # put Sigma into the SumK class
    chemical_potential = SK.calc_mu( precision = prec_mu )  # find the chemical potential for given density
    S.G_iw << SK.extract_G_loc()[0]                         # calc the local Green function
    mpi.report("Total charge of Gloc : %.6f"%S.G_iw.total_density())

    # Init the DC term and the real part of Sigma, if no previous runs found:
    if (iteration_number==1 and previous_present==False):
        dm = S.G_iw.density()
        SK.calc_dc(dm, U_interact = U, J_hund = J, orb = 0, use_dc_formula = dc_type)
        S.Sigma_iw << SK.dc_imp[0]['up'][0,0]

    # Calculate new G0_iw to input into the solver:
    S.G0_iw << S.Sigma_iw + inverse(S.G_iw)
    S.G0_iw << inverse(S.G0_iw)

    # Solve the impurity problem:
    S.solve(h_int=h_int, **p)

    # Solved. Now do post-solution stuff:
    mpi.report("Total charge of impurity problem : %.6f"%S.G_iw.total_density())

    # Now mix Sigma and G with factor mix, if wanted:
    if (iteration_number>1 or previous_present):
        if mpi.is_master_node():
            ar = HDFArchive(dft_filename+'.h5','a')
            mpi.report("Mixing Sigma and G with factor %s"%mix)
            S.Sigma_iw << mix * S.Sigma_iw + (1.0-mix) * ar['dmft_output']['Sigma_iw']
            S.G_iw << mix * S.G_iw + (1.0-mix) * ar['dmft_output']['G_iw']
            del ar
        S.G_iw << mpi.bcast(S.G_iw)
        S.Sigma_iw << mpi.bcast(S.Sigma_iw)

    # Write the final Sigma and G to the hdf5 archive:
    if mpi.is_master_node():
        ar = HDFArchive(dft_filename+'.h5','a')
        ar['dmft_output']['iterations'] = iteration_number
        ar['dmft_output']['G_0'] = S.G0_iw
        ar['dmft_output']['G_tau'] = S.G_tau
        ar['dmft_output']['G_iw'] = S.G_iw
        ar['dmft_output']['Sigma_iw'] = S.Sigma_iw
        del ar

    # Set the new double counting:
    dm = S.G_iw.density() # compute the density matrix of the impurity problem
    SK.calc_dc(dm, U_interact = U, J_hund = J, orb = 0, use_dc_formula = dc_type)

    # Save stuff into the user_data group of hdf5 archive in case of rerun:
    SK.save(['chemical_potential','dc_imp','dc_energ'])

This is all we need for the DFT+DMFT calculation. You can see in this code snippet, that all results of this calculation will be stored in a separate subgroup in the hdf5 file, called dmft_output. Note that this script performs 15 DMFT cycles, but does not check for convergence. Of course, it would be possible to build in convergence criteria. A simple check for convergence can be also done if you store multiple quantities of each iteration and analyze the convergence by hand. In general, it is advisable to start with a lower statistics (less measurements), but then increase it at a point close to converged results (e.g. after a few initial iterations). This helps to keep computational costs low during the first iterations.

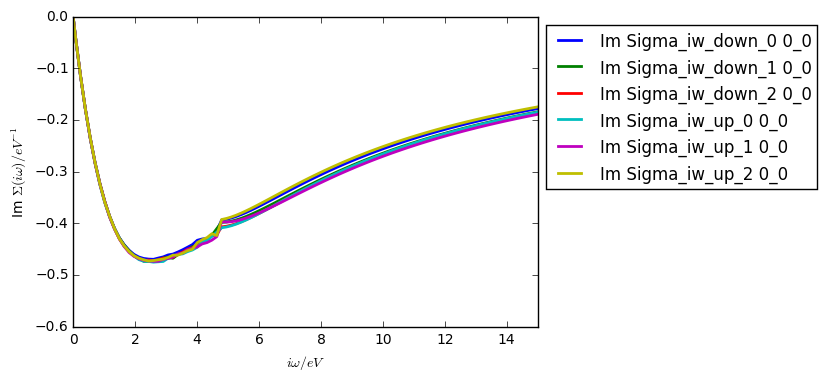
Using the Kanamori Hamiltonian and the parameters above (but on 16 cores), your self energy after the first iteration should look like the self energy shown below.

Tail fit parameters

A good way to identify suitable tail fit parameters is by “human inspection”. Therefore disabled the tail fitting first:

p["perform_tail_fit"] = False

and perform only one DMFT iteration. The resulting self energy can be tail fitted by hand:

for name, sig in S.Sigma_iw:
    S.Sigma_iw[name].fit_tail(fit_n_moments = 4, fit_min_n = 60, fit_max_n = 140)

Plot the self energy and adjust the tail fit parameters such that you obtain a proper fit. The fit_tail function is part of the TRIQS library.

For a self energy which is going to zero for \(i\omega \rightarrow 0\) our suggestion is to start the tail fit (fit_min_n) at a Matsubara frequency considerable above the minimum of the self energy and to stop (fit_max_n) before the noise fully takes over. If it is difficult to find a reasonable fit in this region you should increase your statistics (number of measurements). Keep in mind that fit_min_n and fit_max_n also depend on \(\beta\).