Single-orbital Hubbard model
In this notebook you will reproduce the Bethe lattice DMFT that we did earlier with IPT, but you will use the CTHYB solver to find the solution of the impurity problem. We will consider the problem at half-filling again.
In general it is a good idea to develop the script in the notebook, because it is very convenient to find bugs and to quickly come to a working code. In the beginning you should use a small number of Monte Carlo iterations (say 1000) so that the code runs quickly. Your first main goal is to have a functional script. However, once the script is done, we recommend that you do longer runs (production runs) from a shell. It will be easier for you to see the progress of the Monte Carlo solver. Think about saving the relevant data to an archive and then go back to the notebook when it comes to analyzing and plotting the results. This is usually how things are done: elaboration of the scripts and analysis of the data from the notebook, production from a shell.
In order to run your script from a shell, open a terminal and go in the tutorial directory. This is where you should edit your production script. Let’s call it run_dmft.py. Use your favourite editor (e.g. vi or gedit) to create the script run_dmft.py.
When the script is written save it and run it. You can:
run it directly from the shell to see the Monte Carlo progress:
>>> triqs run_dmft.py
run the following command in a notebook cell.
%run run_dmft.py
That’s it! When the run is done and data has been saved into an archive, you can go back to the notebook and read the archive in order to analyze or plot the results.
Exercise 1
Write a DMFT loop, like you did earlier but using the CTHYB solver.
Hint: It is useful to symmetrize the Green’s function (make the up and down components the same) to avoid some artificial polarization of the system close to the Mott transition. You might want to enforce the up-down symmetry on S.G just before the self-consistency condition. In order to have reasonable data you should have at least 10000 cycles.
Solution 1
The solution of this exercise is in the script scripts/one_band.py in the tutorial directory. We have loaded this script into the cell below.
[ ]:
# %load scripts/one_band.py
from triqs.gf import *
from triqs.operators import *
from h5 import *
from triqs_cthyb import Solver
import numpy as np
# Parameters of the model
t = 1.0
beta = 10
n_loops = 10
# Construct the impurity solver
S = Solver(beta = beta, gf_struct = [('up',1), ('down',1)] )
# I run for several values of U
for U in np.arange(1.0, 9.0):
print('U =', U)
# This is a first guess for G
S.G_iw << SemiCircular(2*t)
# DMFT loop with self-consistency
for i in range(n_loops):
print("\n\nIteration = %i / %i" % (i+1, n_loops))
# Symmetrize the Green's function and use self-consistency
g = 0.5 * ( S.G_iw['up'] + S.G_iw['down'] )
for name, g0 in S.G0_iw:
g0 << inverse( iOmega_n + U/2.0 - t**2 * g )
# Solve the impurity problem
S.solve(h_int = U * n('up',0) * n('down',0), # Local Hamiltonian
n_cycles = 10000, # Number of QMC cycles
n_warmup_cycles = 5000, # Warmup cycles
)
# Save iteration in archive
with HDFArchive("data/one_band/half-U%.2f.h5"%U) as A:
A['G-%i'%i] = S.G_iw
A['Sigma-%i'%i] = S.Sigma_iw
The script saves the Green’s functions and self-energies in archives in the subdirectory called results. They will be used for the analysis below. We study several values of \(U\) to see how the Green’s functions will change. Note that these runs takes a bit of time!
You can
run this directly from the shell to see the Monte Carlo progress or
run the command below.
[ ]:
%run scripts/one_band.py
Exercise 2
Here, you will learn to analyze the output of the solver. As discussed, the Monte Carlo algorithm provide results on the Matsubara axis. This makes the analysis of the results slightly more delicate than if we had them directly on the real axis. When we used the IPT solver, we could see the Mott transition as the appearance of a gap in the spectral function. After the Monte Carlo run, we do not have the spectral function, so we will have to use some other criteria to decide, e.g., if the system is metallic or insulating.
Plot the Green’s function at the end of the DMFT loops for several values of \(U\) (say between 2 and 8). Focus on the extrapolation of the imaginary part of the Green’s function to zero frequency. How does it change with \(U\)? Is there a way to see the Mott transition just by inspecting the imaginary part of the Green’s function?
Solution 2
Start by reading the data from the archive and plot it.
[ ]:
from triqs.gf import *
from h5 import HDFArchive
%matplotlib inline
from triqs.plot.mpl_interface import plt,oplot
import matplotlib as mpl
mpl.rcParams['figure.dpi']=100
A1 = HDFArchive("data/one_band/half-U2.00.h5", 'r')
A2 = HDFArchive("data/one_band/half-U6.00.h5", 'r')
# Plot the Green's function of the last iteration
oplot(A1['G-9']['up'], 'x', label='U = 2.0')
oplot(A2['G-9']['down'], 'o', label='U = 6.0')
plt.xlim(0,10)
plt.show()
As you can see, the behavior of the imaginary part is very different for the two values of \(U\). When \(U\) is small, the system is a metal and the imaginary part extrapolated to zero goes to a finite value. Instead, for large \(U\), the system is a Mott insulator and the imaginary part goes to zero. The reason is that the extrapolation to zero is directly proportional to the density of states at the chemical potential. If the system is gapped, the density is zero; if the system is a metal, there is spectral weight and the density is finite. Therefore, even on the Matsubara axis, one has a way to decide if the system is metallic or not.
Exercise 3
Do the same exercise as above, but analyze the self-energy. The noise usually gets bigger for larger frequencies, so just focus on the first few Matsubara frequencies. There the noise should not be too important. Again, by looking at the extrapolation to zero frequency of the imaginary part of the self-energy, can you tell where the Mott transition happens?
Solution 3
We now do the same for the self-energy.
[ ]:
A1 = HDFArchive("data/one_band/half-U2.00.h5", 'r')
A2 = HDFArchive("data/one_band/half-U6.00.h5", 'r')
# Plot the self-energy of the last iteration
oplot(A1['Sigma-9']['up'].imag, 'x', name='U = 2.0')
oplot(A2['Sigma-9']['up'].imag, 'o', name='U = 6.0')
plt.xlim(0,5)
plt.ylim(-30,0)
plt.show()
Exercise 4
A very useful quantity to measure the degree of correlation of a metal is the quasiparticle weight \(Z\). It is defined as
For a non-interacting metal \(Z=1\). As correlations appear, \(Z\) gradually gets smaller. It reaches 0 at the Mott transition. Make a plot of \(Z\) versus \(U\) for the Bethe lattice Hubbard model.
Hint: In order to have access to the values of \(\Sigma_\uparrow(i\omega_n)\), you can use S.Sigma['up'](n). This will be useful to numerically compute the derivative required to compute \(Z\).
Solution 4
We estimate the derivative using the following approximation
with \(\omega_0 = \pi / \beta\) being the first Matsubara frequency.
[ ]:
import numpy as np
beta = 10
U_list = []
Z_list = []
for U in np.arange(1.0, 9.0):
A = HDFArchive("data/one_band/half-U%.2f.h5"%U, 'r')
Sigma = A['Sigma-9']
Z = 1 / (1 - (Sigma['up'](0)[0,0].imag * beta / np.pi))
U_list.append(U)
Z_list.append(Z)
plt.plot(U_list, Z_list, '-o')
plt.xlabel('U')
plt.ylabel('Z')
plt.show()
Exercise 5
Go back to your IPT code and try to modify it to extract the \(Z\) versus \(U\) curve. Compare this to the result you found in Exercise 4. Is the critical \(U\) for the Mott transition similar to the one you found using CTHYB?
Solution 5
This is just the same script as we had earlier. We just add a couple of lines to extract \(Z\).
[ ]:
from triqs.gf import *
from triqs.plot.mpl_interface import *
class IPTSolver:
def __init__(self, beta):
self.beta = beta
# Matsubara frequency Green's functions
iw_mesh = MeshImFreq(beta=beta, S='Fermion', n_iw=1001)
self.G_iw = Gf(mesh=iw_mesh, target_shape=[1,1])
self.G0_iw = self.G_iw.copy() # self.G0 will be set by the user after initialization
self.Sigma_iw = self.G_iw.copy()
# Imaginary time
tau_mesh = MeshImTime(beta=beta, S='Fermion', n_tau=10001)
self.G0_tau = Gf(mesh=tau_mesh, target_shape=[1,1])
self.Sigma_tau = self.G0_tau.copy()
def solve(self, U):
self.G0_tau << Fourier(self.G0_iw)
self.Sigma_tau << (U**2) * self.G0_tau * self.G0_tau * self.G0_tau
self.Sigma_iw << Fourier(self.Sigma_tau)
# Dyson
self.G_iw << inverse(inverse(self.G0_iw) - self.Sigma_iw)
t = 1.0
beta = 10
n_loops = 30
S = IPTSolver(beta = beta)
U_list2 = []
Z_list2 = []
for U in np.arange(0.0, 9.0):
S.G_iw << SemiCircular(2*t)
for i in range(n_loops):
S.G0_iw << inverse( iOmega_n - t**2 * S.G_iw )
S.solve(U = U)
Z = 1 / (1 - (S.Sigma_iw(0)[0,0].imag * beta / np.pi))
U_list2.append(U)
Z_list2.append(Z)
print(Z)
plt.plot(U_list2, Z_list2, '-o', label='IPT')
plt.plot(U_list, Z_list, '-x', label='CTQMC')
plt.xlabel('U')
plt.ylabel('Z')
plt.legend()
plt.show()
Exercise 6
Try to analytically continue the Green’s function on the real axis using the Pade approximation. What can you say about the result?
Solution 6
[ ]:
from math import pi
with HDFArchive("data/one_band/half-U4.00.h5", 'r') as A:
g = A['G-9']['up']
g_real = GfReFreq(indices=[0], window=[-5,5])
g_real.set_from_pade(g)
oplot(-g_real.imag/pi)
plt.show()
The result is completely wrong. This is because of the noise in the Monte Carlo data. One would have to make much longer runs in order to reduce the error bars. The Pade approximation can be used only on very accurate data. When the noise is still quite large, one has to use different analytical continuation methods, like MaxEnt, which produces the following spectral function:
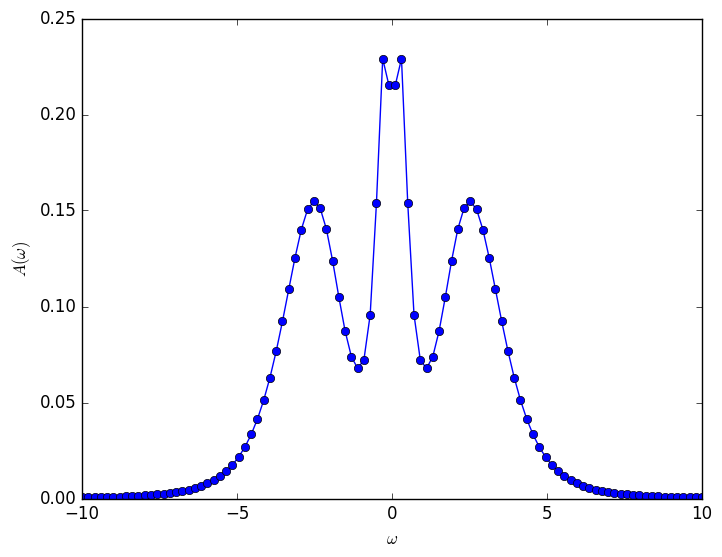
Regardless of which package you use for MaxEnt, it is very important to remember that there are some important knobs with which one can play in MaxEnt that can substantially change the results, and so one must be very careful in its use!
Exercise 7
In the last exercise we will analyze the impurity multiplets, the many-body states and their occupancies, using the CTHYB solver. To do this, we instruct the solver to measure the many-body density matrix of the impurity during sampling. This can be done at almost no additional numerical cost in CTHYB by passing the options measure_density_matrix = True and use_norm_as_weight = True to the solve call of the solver.
Write a small script that measures the impurity density matrix for two U-values (metallic and insulating) and analyzes/compares the two solutions by saving the solver object after convergence is reached for both values. Then you can access the density matrix as S.density_matrix. We provide a function to analyze the multiplets within CTHYB: triqs_cthyb.multiplet_tools.multiplet_analysis. Have a look at the
documentation to better understand how to use it. Use the code from exercise one to do this by extending it.
The function multiplet_analysis will also characterize each impurity many-body state with its quantum numbers. What is the characteristic feature in the multiplet structure of the Mott insulating state?
Tip: By default, printing a panda’s data frame shows all stored multiplets sorted by occupation probability.
[ ]:
# Parameters of the model
t = 1.0
beta = 10
n_loops = 10
# Construct the impurity solver
S = Solver(beta = beta, gf_struct = [('up',1), ('down',1)] )
# run metallic U
U = 2.0
# This is a first guess for G
S.G_iw << SemiCircular(2*t)
# DMFT loop with self-consistency
for i in range(n_loops):
print("\n\nIteration = %i / %i" % (i+1, n_loops))
# Symmetrize the Green's function and use self-consistency
g = 0.5 * ( S.G_iw['up'] + S.G_iw['down'] )
for name, g0 in S.G0_iw:
g0 << inverse( iOmega_n + U/2.0 - t**2 * g )
# Solve the impurity problem
S.solve(h_int = U * n('up',0) * n('down',0), # Local Hamiltonian
n_cycles = 10000, # Number of QMC cycles
n_warmup_cycles = 5000, # Warmup cycles
measure_density_matrix = True,
use_norm_as_weight = True
)
solver_U_met = S
################################
U = 8.0
S = Solver(beta = beta, gf_struct = [('up',1), ('down',1)] )
# This is a first guess for G
S.G_iw << SemiCircular(2*t)
# DMFT loop with self-consistency
for i in range(n_loops):
print("\n\nIteration = %i / %i" % (i+1, n_loops))
# Symmetrize the Green's function and use self-consistency
g = 0.5 * ( S.G_iw['up'] + S.G_iw['down'] )
for name, g0 in S.G0_iw:
g0 << inverse( iOmega_n + U/2.0 - t**2 * g )
# Solve the impurity problem
S.solve(h_int = U * n('up',0) * n('down',0), # Local Hamiltonian
n_cycles = 10000, # Number of QMC cycles
n_warmup_cycles = 5000, # Warmup cycles
measure_density_matrix = True,
use_norm_as_weight = True
)
solver_U_ins = S
[ ]:
# import and use multiplet analysis function to get panda data frame of the impurity multiplets
from triqs_cthyb.multiplet_tools import multiplet_analysis
[ ]:
# using now the multiplet analysis function to obtain a panda data frame of the occupied multiplets
res_met = multiplet_analysis(rho = solver_U_met.density_matrix,
h_loc_diag = solver_U_met.h_loc_diagonalization,
# one orbital
n_orb = 1,
# two spin channels
spin_names = ['up','down'])
res_met
[ ]:
res_ins = multiplet_analysis(rho = solver_U_ins.density_matrix,
h_loc_diag = solver_U_ins.h_loc_diagonalization,
n_orb = 1,
spin_names = ['up','down'])
res_ins
We observe that in the insulating state only the high spin states with \(m_s= \pm 0.5\) are occupied, while in the metallic state also the low spin states with \(m_s=0.0\) are occupied. We can also see that their relative energy eigenvalues within the impurity change when U is varied.