A tight-binding model on a square lattice
Let us now consider free fermions on a Bravais lattice.
We will set up a square lattice with the nearest
neighbour hopping using the BravaisLattice class of TRIQS, compute its
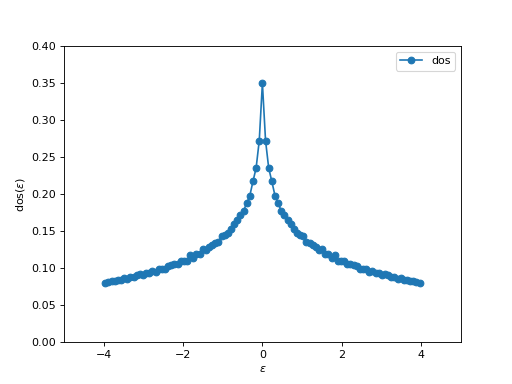
density of states (DOS) and then plot it by using again the oplot function.
from triqs.lattice.tight_binding import *
# Define the Bravais Lattice : a square lattice in 2d
BL = BravaisLattice(units = [(1,0,0) , (0,1,0) ])
# Prepare a nearest neighbour hopping on BL
t = -1.00 # First neighbour Hopping
tp = 0.0*t # Second neighbour Hopping
# Hopping[ Displacement on the lattice] = [[t11,t12,t13....],[t21,t22,t23....],...,[....,tnn]]
# where n=Number_Orbitals
hop= { (1,0) : [[ t]],
(-1,0) : [[ t]],
(0,1) : [[ t]],
(0,-1) : [[ t]],
(1,1) : [[ tp]],
(-1,-1): [[ tp]],
(1,-1) : [[ tp]],
(-1,1) : [[ tp]]}
TB = TightBinding ( BL, hop)
# Compute the density of states
d = dos (TB, n_kpts= 500, n_eps = 101, name = 'dos')[0]
# Plot the dos it with matplotlib
from triqs.plot.mpl_interface import oplot
from matplotlib import pylab as plt
oplot(d,'-o')
plt.xlim ( -5,5 )
plt.ylim ( 0, 0.4)
(Source code, png, hires.png, pdf)
More information on the lattice tools implemeted in TRIQS can be found here.