Manipulating fermionic operators

Before we see how to use a CTQMC impurity solver, it will be useful to learn about operators. Indeed, one of the inputs of the CTQMC solver is a Hamiltonian in operator form.

Fundamental operators

After importing the operator module, the keyword c_dag and c allow to define a new fermionic operator. c_dag and c are followed by two indices. Inspired by the block structure of Green’s functions, the first index is a block index, while the second is the index within the block. Here’s an example of operators as they would be defined if we had two blocks up and down of size 1:

from triqs.operators import c, c_dag, n, Operator # n and Operator will be needed later
print(c_dag('up',0))
print(c('up',0))
print(c_dag('down',0))
print(c('down',0))

1*c_dag('up',0)
1*c('up',0)
1*c_dag('down',0)
1*c('down',0)

Number operator

The keyword n is defined as \(C^\dagger C\)

print(n('up',0))

1*c_dag('up',0)*c('up',0)

Operations with operators

Operators can be manipulated and anti-commutation relations will be used to simplify expressions

# Should give 0
print(n('up',0) - c_dag('up',0)*c('up',0))

0

# Some calculation
print(n('up',0) - 2 * c_dag('up',0)*c('up',0))

-1*c_dag('up',0)*c('up',0)

# Define the parameters
U = 4
mu = 3

# H is an empty operator
H = Operator()

# Add elements to define a Hamiltonian
H += U * n('up',0) * n('down',0)
H -= mu * (n('up',0) + n('down',0))
print(H)

-3*c_dag('down',0)*c('down',0) + -3*c_dag('up',0)*c('up',0) + 4*c_dag('down',0)*c_dag('up',0)*c('up',0)*c('down',0)

Exact Diagonalization

For small system-sizes we can use AtomDiag provided by TRIQS to perform exact diagonalization on the Hamiltonian

from triqs.atom_diag import AtomDiag
?AtomDiag

Signature: AtomDiag(*args, **kwargs)
Docstring:
Lightweight exact diagonalization solver

Use the QR algorithm to diagonalize the Hamiltonian.
Auto-partitions the Hamiltonian into subspaces (blocks)
such that all creation and annihilation operators map one
subspace to exactly one other subspace.

Parameters
----------
h: Operator
    Hamiltonian to be diagonalized.
fops: list of tuple of strings and ints
    List of all annihilation / creation operator flavors (indices).
    Must at least contain all flavors met in `h`.
qn_vector: list of Operator, optional
    Vector of quantum number operators to be used for the auto-partitioning
n_min, n_max: integers, optional
    Truncate the Fock-space to states with particle number in [n_min, n_max]
    Cannot be combined with qn_vector
File:      ~/opt/triqs/lib/python3.11/site-packages/triqs/atom_diag/__init__.py
Type:      function

# List of operator flavors
fops = [('up',0), ('down',0)]

# Construct AtomDiag object, Performs diagonalization
AD = AtomDiag(h=H, fops=fops)

print(AD.gs_energy)

-3.0

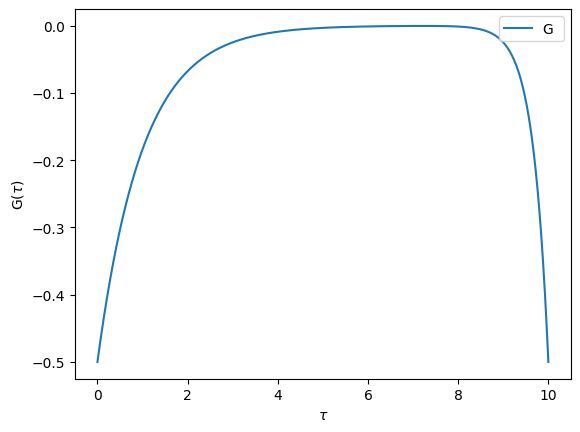
We can then use the AtomDiag object to obtain for example the atomic Green’s functions

from triqs.atom_diag import atomic_g_tau
Gtau = atomic_g_tau(atom=AD, beta=10, gf_struct=[('up',1),('down',1)], n_tau=1001)

from triqs.plot.mpl_interface import oplot
%matplotlib inline
oplot(Gtau["up"][0,0].real, name='G')